Bb soprano saxophone

C#5

Impedance

Fingering a key depressed a key not depressed a hole covered a hole uncovered a part of the mechanism that is not normally touched Details in fingering legend. Acoustic schematic a closed tone hole an open tone hole Non-specialist introduction to acoustic impedance Non-specialist introduction to saxophone acoustics Notes are the written pitch. Frequencies are the sounding frequency, for Bb saxophone. Unless otherwise stated, the impedance spectrum is for a Bb saxophone.

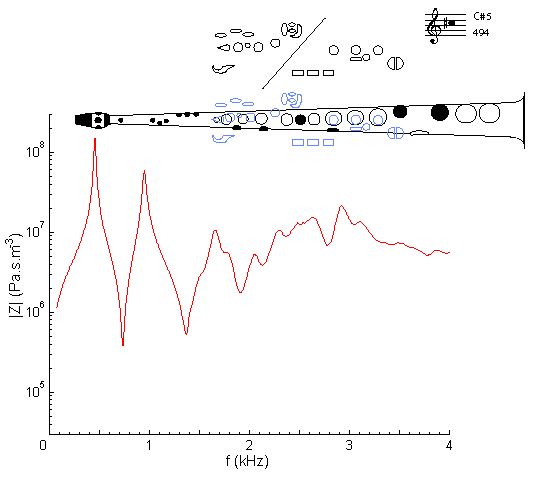
At frequencies below about 1 kHz, this curve looks rather like that for C5, but raised in frequency. At higher frequencies, however, the situation is complicated by the cut-off frequency. Here we have only two peaks that fall in the harmonic series: this fingering will bugle an octave, but no other note in the series. The first peak can be reduced in magnitude and shifted in frequency using a register hole (operated by the octave key): see C#6.

For general comments about the first register, see A#3. Compare with the impedance spectrum for a tenor sax on written C#5: same fingering but sounding one octave lower.

Sound

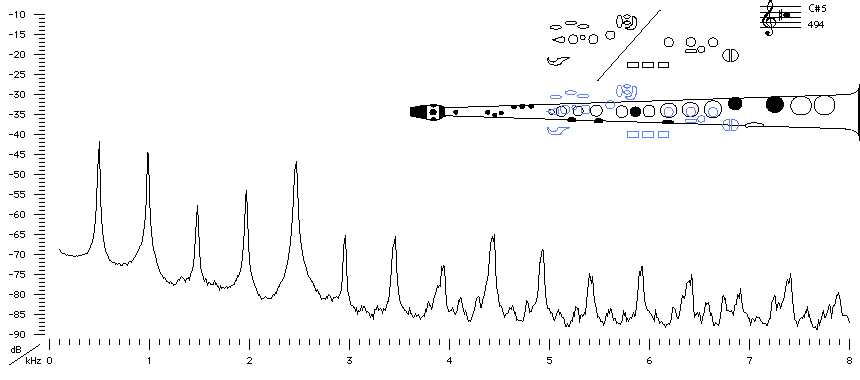
Sound spectrum of a Bb soprano saxophone played using fingering for C#5.
For more explanation, see Introduction to saxophone acoustics.

Sound Clip

You can hear C#5 played.

Impedance

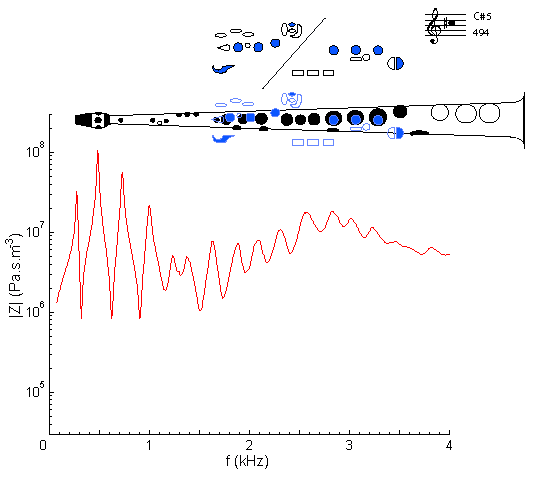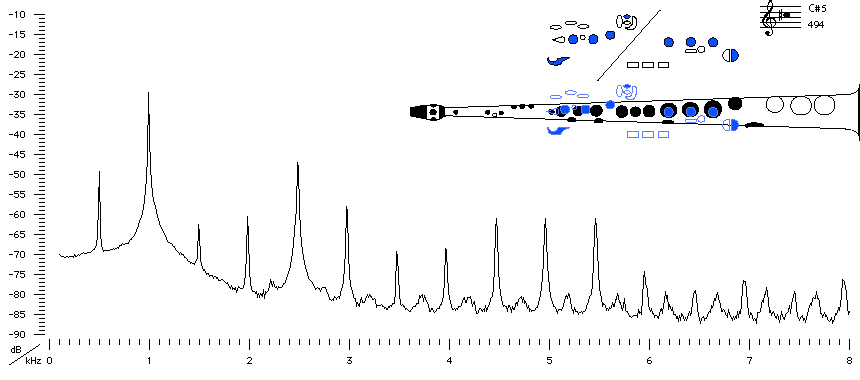
This is the first fingering (albeit an alternative one) for a note in the second register – meaning that it plays at the second peak on the impedance spectrum. It differs from C#4 (the corresponding note in the first register) in that it uses a register hole (operated by the octave key). This causes a leak in the bore that weakens (and mistunes) the first impedance peak, but has little affect on higher peaks – see register hole for an explanation, and compare with C#4. This impedance spectrum is almost identical to that for C#4, including the frequencies above the cut-off frequency, except for the first peak which is weakened and sharpened slightly, thus the reed sounds at the second peak instead, an octave above.

Sound

Sound Clip