Membrane homeostasis
(and tension regulation, cell area regulation, mechanosensitive membrane exchange, membrane traffic and osmotic response)

photo of protoplast partially inspired in a pipette

Membrane mechanical homeostasis, tension regulation, area regulation and mechanosensitive membrane traffic are all used to describe membrane-reservoir exchange, a phenomenon that complicates membrane mechanics, osmosis and cellular osmotic response.

Some cell membranes, when exposed to increased tension, increase their area by incorporating new membrane material from a reservoir. Conversely, when the tension is sufficiently low, they may delete material from the membrane, and thus sometimes regain their original shape after, for example, osmotic contraction. One important consequence is the lysis of cells during cycles of osmotic contraction and expansion.

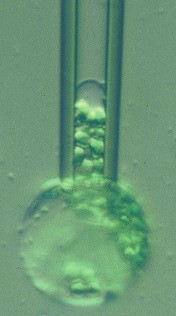
The figure at right shows a plant protoplast (from a rye leaf) in a micropipette. Large changes in area can be imposed by osmotic pressure variation or by micropipette aspiration (as here). These and some other cells survive huge variations in membrane area: how do they survive these variations without lysis?

Colleague Peter Steponkus and I proposed the mechanosensitive mechanism in the early 1980s. In this page we reproduce some of the data that led us to this model, including plots of how the incorporation rate depends on the membrane tension. We also list the original papers, some of them available in .pdf format.

This phenomenon has recently been observed in a range of cell types. Following its more recent observation in mammalian cells, there has been increased interest in the phenomenon, and it has been given a variety of new names.

What is the membrane reservoir?

The sketches below illustrate the model we proposed and one of the reservoir types we observed in protoplasts. Over a time of minutes, in the absence of osmotic or mechanical stresses (first sketch), the protoplast becomes spherical and has an equilibrium or resting tension γr in the membrane, which is typically 0.1 mN/m. (To put this value in context, the surface tension of water is approximately 74 mN/m. It is much easier to suck a cell into a pipette than to suck an air bubble in.) We proposed that the membrane's resting tension is established by a dynamic equilibrium between the incorporation of new material into the membrane, and an equal rate of transfer of membrane material from the membrane into a reservoir, which in this case is shown as cytoplasmic vesicles.

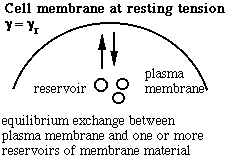
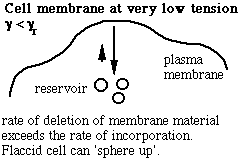
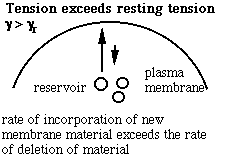
schematic of membrane exchange at resting tension     schematic of membrane exchange at low tension     schematic of membrane exchange at high tension    

Schematic of the membrane-reservoir exchange at different values of membrane tension. (Vesicles are not the only reservoir: membrane folds or rafts are other possibilities, as are tethers linking the membrane to internal membrane structures. Monomers of membrane material are also a possible reservoir, but the rates of monomer exchange would probably be very slow for living membranes.)

How does membrane area vary with tension and time?

The experimental results that led us to postulate this model are shown below. The figure below (Wolfe & Steponkus, 1983) shows the area response to controlled tension, imposed with a micropipette. The membranes we studied could expand by about 2% in area during a rapid expansion (i.e. over several seconds). For rapid changes over this range, the fractional change in area was approximately proportional to the change in the imposed tension. The relevant elastic constant of the membrane is the area elastic modulus, ka (the ratio of change in tension to fractional increase in area). Its value is about 230 mN/m for these protoplast. However, area changes much greater than a few percent are possible if there is time for the exchange of membrane material, as this figure shows.  

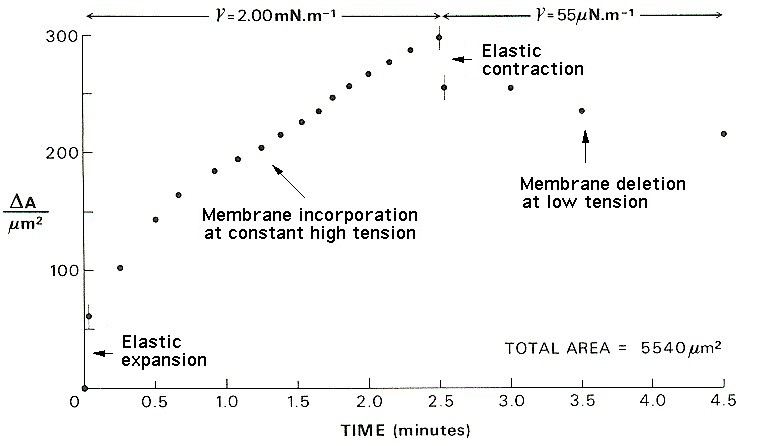
The response of the membrane area to increase, constant, decrease and constant tension

Response of the cell membrane area to step increase, constant high tension, step decrease and constant low tension, imposed with a micropipette.

Note that, when the membrane tension is increased by 2 mN/m at t = 0, the area increases very quickly by about 1%. This is an elastic response: it is readily and rapidly reversible. Next, the membrane tension is maintained at a constant level, well above the resting value, for 2.5 minutes. During this period, the membrane area increases at a roughly constant rate, as new material is incorporated. At t = 2.5 minutes, the membrane tension is suddenly reduced to a value below the resting value. There is a rapid elastic decrease in area of about 1%. While the tension is maintained at a low value, material is lost from the plane of the membrane and its area steadily decreases. Typical protoplasts could survive area increases of tens of percent, and some individual cells could survive hundreds of percent.

For the results shown in the figure below, also from Wolfe & Steponkus (1983), the membrane tension was increased to a value close to the level required to rupture it. Thereafter, the suction in the pipette was adjusted so as to keep the membrane area constant. The tension falls rapidly at first, because the rate of incorporation into the membrane is high. The incorporation of new material reduces the stretching and so lowers the tension, so the rate of incorporation gradually falls over time.

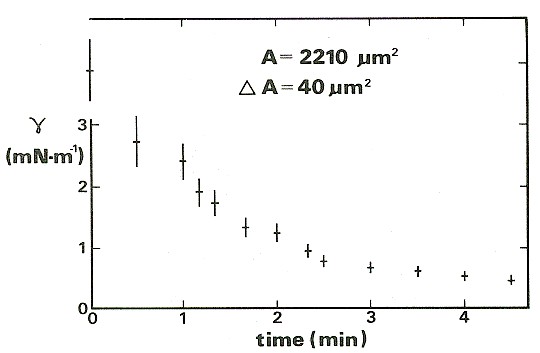
Graph of the response of the membrane tension to a step increase in area

Relaxation of the membrane tension and approach to equilibrium in a cell maintained at constant area using a micropipette.

This is a marked contrast to the elastic response to rapid changes (see the previous figure). Here we see that, after a long time, the membrane tension returns to its resting value. Thus

How does the rate of incorporation depend on the tension in the membrane?

In a further study (Wolfe, Dowgert & Steponkus 1985), again using micropipettes, we applied to the cell membrane tensions which increased at a range of different rates (the parameter β in the figure below), while we measured the area increase in the membrane. We analysed the data to obtain the incorporation rate as a function of tension. The results are shown below.

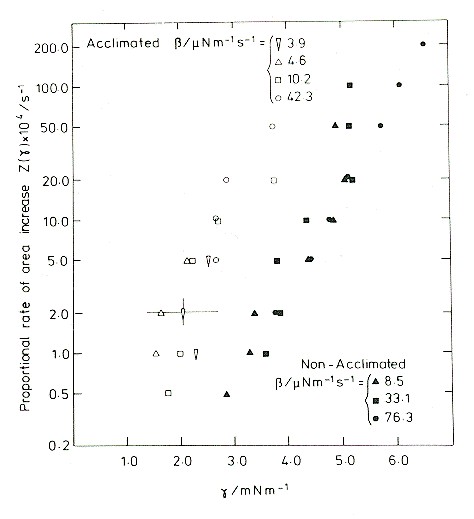
membrane area expansion rate as a function of tension

Membrane incoroporation rate as a function of tension.

The data on this semilog graph fall approximately in straight lines. So, over this range of tensions, the rate of incorporation of new material increases approximately exponentially with tension. The vertical scale covers the range 0.002% per second to 2% per second, but the tensions required to produce the latter rate are quickly fatal. Indeed, all of these experiments ended in rupture, which determined the upper limit of tensions measured. There are two data sets: the filled symbols are for protoplasts obtained from rye seedlings grown under mild conditions, and the open symbols for protoplasts obtained from seedlings that had been cold acclimated. The acclimated plants were frost resistant, and their tissues were able to withstand a freeze-thaw cycle. Protoplasts extracted from the acclimated plants were better able to withstand a large cycle of osmotic contraction and expansion, such as is produced in the extracellular medium by a freeze-thaw cycle.

What is the reservoir and what are the mechanism and kinetics for exchange? We suggested cytoplasmic vesicles (larger ones might be tethered to the membrane) and submicroscopic membrane folds and extrusions. For simpler systems such as artificial bilayers, thermodynamic equilibration is possible, and we describe these for such systems (Gruen and Wolfe, 1982; Wolfe, 2015). However, the mechanisms involved in living cells may not be equilibrated under most conditions and the exchange process may be complicated.

So how did this phenomenon affect protoplasts and what are its implications for freezing tolerance? As shown in the previous figure, protoplasts from acclimated seedlings incorporated membrane material at a much greater rate, for any given membrane tension, than did those from non-acclimated plants. This explains their increased frost resistance. The reservoirs of the two were different: internal vesicles for the normal, and exocytotic extrusions for the acclimated. The next step was to analyse the problem quantitatively.

Implications for surviving osmotic changes and freezing.

The probability of membrane lysis also depended nearly exponentially on the membrane tension (Wolfe, Dowgert & Steponkus 1985) and the parameters to characterise this dependence were obtained from the same expansion histories as were used in the previous figure. So this was a very pretty biophysical problem: we had measured directly the elastic and fragility properties of the membrane, and also the dynamics of the membrane exchange. We had measured the hydraulic permeability of the membrane, and we knew the osmotic pressure changes to which we were exposing the protoplasts. Thus, as shown in the schema below, we were able to obtain an (analytical) expression for the chance of survival of a given osmotic pressure excursion. And there were no external parameters to fit!

schematic of solving the survival problem

A schematic of solving the freezing survival problem.

Joe Wolfe, School of Physics, The University of New South Wales, Sydney

This work was done when I was a postdoc with the late Peter Steponkus at Cornell University. Michael Dowgert was a PhD student at the time, and he carried on the project after the Ithaca winters drove me back to Oz.

References A list of publications by Joe Wolfe.
Cryobiology links

© 2005. Modified 27/1/05 J.Wolfe@unsw.edu.au, phone 61- 2-9385 4954 (UT + 10, +11 Oct-Mar).
Joe Wolfe, School of Physics, University of New South Wales, Sydney, Australia.

Joe's scientific home page
Joe's educational pages
Joe's music page

Pic of the author