| Acoustics of the saxophone |
Bb soprano saxophone |
A#3 |
|
Fingering Acoustic schematic Non-specialist introduction
to acoustic impedance Notes are the written pitch. |
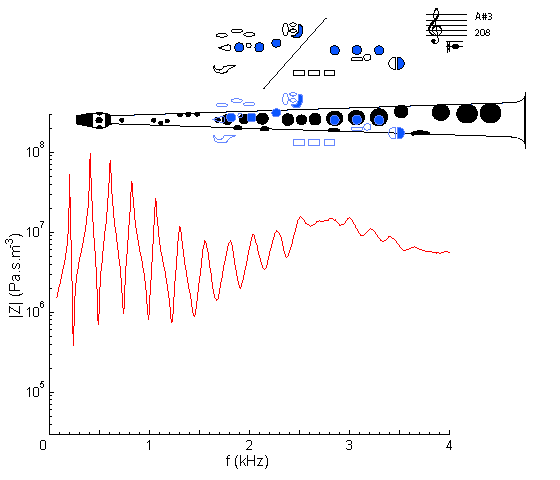
This is the lowest note on this saxophone. All tone holes are closed, so the sax most closely resembles a conical pipe. The maxima fall at frequencies in approximately harmonic series: frequencies f, 2f, 3f etc. (For a detailed explanation and comparison of conical and cylindrical closed and open pipes, see Pipes and harmonics.) As a result, the regular series of maxima (and minima) in Z(f) extends to high frequencies.
The maxima (and minima) become weaker at high frequencies for several reasons: first, the loss of energy where the moving air is close to the walls is more important at high frequency. Second, the bell radiates high frequencies better than low, so there is less reflection of high frequencies and so weaker resonances. However, the first maximum is weaker than the next. This is due to the conical shape. For a simplified explanation, and to understand how the bell and the mouthpiece contribute to the shape of this curve, see frequency response and acoustic impedance in Saxophone acoustics. At very high frequencies, the conical shape and the bell radiate so well – rather like a megaphone – that there is very little reflection and so no resonances and no impedance peaks.
The first several maxima can be played – it's called bugling: the resonance associated with each peak drives the reed. However, the first maximum is more difficult to play than the next, especially when playing softly. Loud notes have disproportionately more contribution from high harmonics, and the high harmonics of the lowest note match impedance peaks, while a soft note has less 'help' from higher harmonics.
Compare with the impedance spectrum for a tenor sax on written A#3: same fingering but sounding one octave lower.
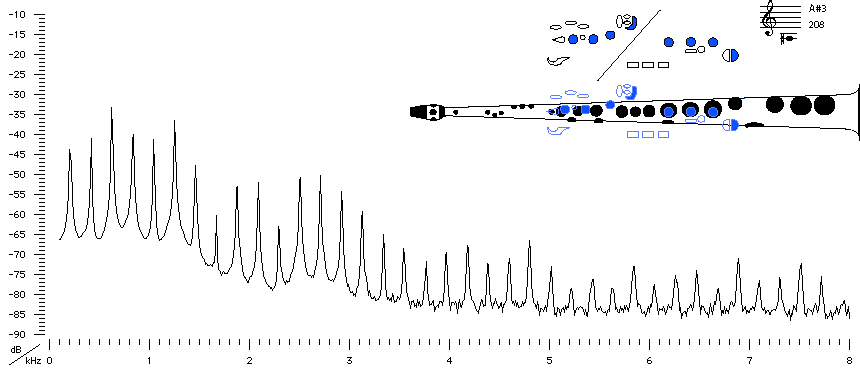
Sound spectrum
of a Bb soprano saxophone
played using fingering for A#3.
For more explanation, see
Introduction to saxophone acoustics.
The peaks in the sound spectrum are harmonics: they fall at frequencies f0, 2f0, 3f0, etc. This is only approximately true of the peaks in the impedance spectrum, and the difference becomes more pronounced the higher we go in the registers. Here, the first several (approximately) harmonic resonances of the bore are all involved in driving the reed at f0, which is close to a common factor of the frequencies of the impedance peaks. The vibration of the reed and the acoustic component of the air flowing past it involve nonlinear processes, such as the turbulent loss of kinetic energy of the air. This nonlinearity is what produces the higher harmonics. The reed motion becomes very nonlinear when it begins to strike the lay. At this dynamic level, the power of the fundament at f0 changes relatively little, and blowing harder instead adds more power to the higher harmonics, making the sound brighter. In its low range, and especially when played loudly, the fundamental of the saxophone is often weaker than some of the harmonics, in part due to the relatively weak first impedance peak. For more detail, see What is a sound spectrum?
The relatively weak impedance peaks at low frequencies are due to the conical bore. Very informally, we could say that, because low frequencies have long periods, there is time for air to flow from the confined cross section of the bore at the mouthpiece down to where the bore has a larger diameter. So the typical impedances are low in this range. This does make the low notes of the saxophone a bit difficult to play – especially to play softly, when one relies less on the higher resonances to 'help' the fundamental vibration. On the other hand, the conical bore does radiate well and makes the instrument loud overall, which was one of the reasons for its invention.
In the case of notes in the lower range of the instrument, several of the harmonics coincide with resonances - peaks in the impedance spectrum. This means that the bore helps radiate them strongly. For high harmonics (say above 2.5 kHz), there are no corresponding strong resonances. However, these radiate fairly well anyway, because the saxophone is a reasonably good megaphone at these frequencies.
In the sound spectra for the low notes, we can notice a sudden increase in the negative slope of the spectral envelope that occurs close to the cut-off frequency of about 1.2 KHz.
Wind and bowed string instruments differ from percussion and plucked strings, in the the former have exactly harmonic spectra. See the discussion in How harmonic are harmonics?
|
Contact:
Joe Wolfe
/ J.Wolfe@unsw.edu.au |