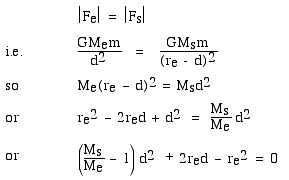Why doesn't the moon fall into the sun at new moon?

Suppose that it is noon. You jump up, and you fall back towards the earth. You do not fall into the sun. No surprise: although the sun is much more massive than the earth, it is much further away, so, near the surface of the earth, the gravitational field of the earth is much stronger than that of the sun.

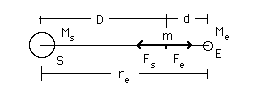
So, how high would you have to go before the sun's gravitational attraction would win? At what point, on a line between the earth and the sun, are the two gravitational forces exerted by the sun and the earth equal and opposite? Let's say it is at a point d from the centre of the earth, and D from the centre of the sun. Obviously d is much less than D because the sun's mass (M_s = 1.99 x 10³⁰ kg) is much greater than the mass of the earth (M_e = 5.98 x 10²⁴ kg). But just how far away is that point at d? For the calculation, we shall need the distance between the earth and the sun, which on average is r_e = 1.50 x 10⁸ km.

Let's draw a diagram -- not to scale at first, because we still haven't done the calculation: let's put a mass m at distance d from the moon and D from the sun.

diagram of sun, moon and the point of equal attraction

Now we just set the magnitude of the two gravitational forces, acting on a mass m, equal to each other:

equations to calculate the point of equal field

When we solve the quadratic, we get 260,000 km. (If you don't trust me, check it yourself.)

The puzzle:

Now the moon is 380,000 km from the earth. At new moon, it lies nearly on a line between the earth and the sun (during a solar eclipse, it lies exactly on this line). So, at new moon, will the moon fall into the sun? Choose one of these answers:

The calculation above is wrong: the moon will not be accelerating towards the sun, so there is nothing to worry about. [Explain error in the above.]
The moon will be accelerating towards the sun but there is nothing to worry about because [insert plausible reason].
The moon will be accelerating towards the sun so my friend and I shall experience our last moonrise together over the ocean and we'll then sell our shares in tidal power stations.

Some links

An introduction to Netwon's laws and gravity.
Resources for high school physics including the FAQ in high school physics.

© 2005. J.Wolfe@unsw.edu.au, phone 61- 2-9385 4954 (UT + 10, +11 Oct-Mar).
School of Physics, University of New South Wales, Sydney, Australia.

Joe's scientific home page
Joe's educational pages
Joe's music page