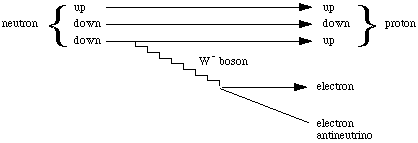
What are the the trigonometric parallax limits for space-based and ground-based methods of measurement?
Parallax refers to the different views that you see from two different positions. Try this experiment. Hold the index finger of your left hand vertical, 20 cm in front of you. Hold the index finger of your right hand vertical, 40 cm in front of you. Now close your left eye and, using just your right eye, move the two fingers sideways until they line up. Now close your right eye and open the left. The closer finger has 'jumped' to the right of the further finger. Repeat a few times. Compared to a distant background, both fingers have both jumped to the right, but the closer one jumps father. If you measure the angles through which they jump and the distance between your eyes, you can work out how far away the fingers are.
For distant objects, the distance between our viewing positions must be greater than the distance between your eyes. Fortunately for astronomers, the Earth shifts our telescopes round the sun once a year, so we can get a separation equal to the diameter of the orbit of the Earth (16 light minutes) if we wait six months, as shown in this diagram.
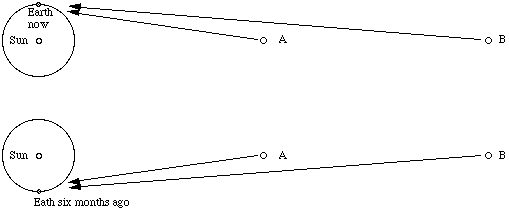
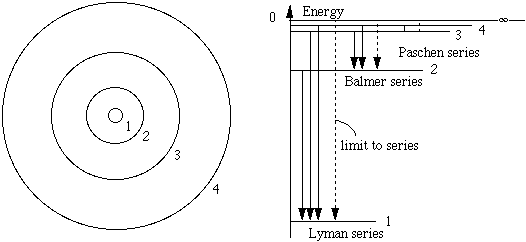
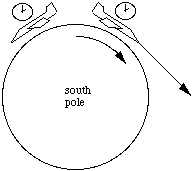
In this sketch, which is not to scale, imagine an observer looking at objects A and B, standing at the pole of the Earth with his head towards us. Now he sees object A to be to the right of B. Six months ago, he saw it to be to the left of B. Now most stars are so far away from us that we cannot observe any relative motion in this way. However, for close stars it is possible. The next sketch shows the path of light from a close object and from a very distant star.

From trigonometry,
where we have used the small angle approximation for θ measured in radians. A parsec is defined as the distance to an object that 'moves' (with respect to the distant stars) by an angle of 1 second (1/3600 of a degree) when the Earth moves by the mean radius of its orbit. In terms of this sketch, if θ = one second, D = 1 parsec. Now all stars except the sun are more than one parsec distant, so to measure their distance by parallax, we need to be able to resolve angles of about 1 second or better. Is this possible?
One limitation to the angular resolution of telescopes is due to a wave effect called diffraction. When parallel light passes is incident on a circular lens or circular telescope with an aperture a, it cannot be focussed onto a perfect point, but rather makes a small circular smudge called the Airy disc. Around this bright circle is a dark ring, then a series of bright and dark rings: the diffraction pattern of a circular aperture. The angular diameter of the central bright ring is of the order of λ/a, where λ is the wavelength of the light (or other waves). If the angular separation between two stars is smaller than the size of this disc (as is the case for the majority of double stars), then it is very difficult to resolve them as two different stars. (In practice, this theoretical limit is not always achieved in optical telescopes because of such effects as the bending of light in the atmosphere.) So an angle of λ/a is approximately the theoretical limit to the angle that can be resolved by a telescope (or camera, or eye*).
Radio telescopes, which use long wavelengths (eg 21 cm, the wavelength of the 'hydrogen line') have to be much bigger than optical telescopes (L ~ 0.0005 mm), but in both cases, the bigger the better. Optical telescopes may have a of several metres. Individual radio telescopes may have a of 10s of m (eg the dish at Parkes is 64 m), but separate radio telescopes may be connected to provide a bigger effective aperture. The Australia Telescope links radio telescopes across the country to provide an effective aperture of thousands of km.
Space based optical telescopes have the advantage that they have no atmospheric distortion and so they can measure smaller angles than ground based ones.
* λ/a is also one of the limits to the angle you can resolve with your eye. This limit is only achieved, however, when your pupil is almost closed (aperture a less than about 2 mm), in very bright light. In dim light, when you pupil is open wider, the angular resolution is typically a bit better than one minute (1/60 degrees), and is determined by the spacing of photoreceptors in your retina (which you can now work out).


.GIF)