|
|
|
| Relativity
in brief... or in detail.. |
Anwers to the Quiz: how well have you understood the Einstein Light presentation?The questions appear with their answers below.Question 1The chemist and the accountant. My chemistry text tells me that 12.000 g of carbon 12 is called a mole and has 6.023 x 1023 atoms. Each atom has six protons, six neutrons and six electrons. When I look up the mass of protons, neutrons and electrons, I find that the whole is less than the sum of the parts. Carbon 12 weighs less than the combined weights of its protons, neutrons and electrons. What is the explanation?
Consequently, it takes work to 'pull a carbon nucleus apart' into its constituent neutrons and protons. This work W increases the mass by an amount Δm where W = Δmc2. Question 2A bus turns a corner to the right and a standing passenger, who is not holding on to the grab rail, falls over. Explain this briefly in terms of Galilean or Newtonian physics.
"Garbage" she says. "Centrifugal forces don't exist. They are called fictitious forces and your explanation is a fictitious explanation." The confrontation escalates and we discover that a policeman has seen the bus turn. "Ah", she says "an observer in an inertial frame of reference: he'll be able to explain it". "Easy" says the policeman , who has just read Inertial frames and why the laws are the same in the train and on the platform, "There was no centrifugal force. You kept travelling in a straight line while the bus, including your squashed interlocutor, turned right. She put her lap immediately under your trajectory.
Question 3Imagine that you are travelling in a spaceship at 99% of the speed of light. You look at your watch. Do you see anything strange? Explain your answer.
Question 4If the laws of physics are the same for two observers in uniform relative motion, why do they get different answers when they calculate physical quantities? Explain briefly, perhaps with an example.
Question 5When Jasper and Zoe board space ships in Energy in Newtonian mechanics and in relativity, why does Jasper's ship change colour and not Zoe's? (Hint: in deep space, where does the light come from?)
This question is arguably a trick question, because of the severe simplifications that have been made in the animations, as discussed in the Caveats. Question 6An astronaut set out in a spaceship from Earth to travel to a distant part of our galaxy. The spaceship travelled at a constant speed of 0.8 c. When the spaceship passed a certain star, the on-board clock showed the astronaut that the journey had taken 10 years. To save you punching a calculator, at the speed 0.8 c, the relativistic factor g = (1-v2/c2)-.5 = 1.7 and its reciprocal is 0.6.An identical clock remained on Earth. What time had elapsed on the Earth clock, when the astronaut's spaceship passes the star?
(B) 6 years (C) 10 years (D) 17 years (E) none of the above (F) any of the above
Question 7A scientist measures the current flowing in two long parallel wires. The flow is in the same direction in each, as in our demonstration. Knowing the density of conduction electrons and the cross section of the wire, she works out the average speed of the electrons in the wire. Let's assume it is the same for all conduction electrons, and zero for all others. The speed v of the conduction electrons is very much smaller than c, as is usually the case. Also, let us neglect the voltage difference along the wire (the resistance of the wire is negligible).She now decides to observe the two wires from a high speed vehicle travelling parallel to the wires, in the direction of the electron travel, at the same speed. Will the force between the two wires be larger, smaller, about the same, or zero? Again, marks for the explanation of the correct answer, not just for the answer. (If the electrons move at speeds that are not << c, then this question becomes much more complicated.)
Question 8A long pendulum is set swinging in a plane, somewhere on the surface of the Earth. An observer notices that the plane of the oscillation of the pendulum appears to rotate anticlockwise such that it appears to be again swinging in the same plane about 12 hours later. Is it raining?
So this pendulum swings at the South Pole, where it never rains. Question 9A train moves at constant, relativistic speed. When the train passes a pole by the track, a clock on board records the time reading. There are two poles. Each has a similar clock, which records when the front of the train passes it. The clocks on the poles have been carefully synchronised.Call Ttrain the interval measured between the readings by the clock on the train, and Ttrack the interval between the readings of the pole clocks. Consider the following statements:
ii) According to relativity, an observer on the train sees the clocks on the poles running slow, so she predicts Ttrack < Ttrain. iii) The two observers can send each other their (already recorded) measurements, at their convenience. They cannot both be correct, so there must be a paradox.
As in the twin paradox, there is no symmetry, so no paradox. Question 10Zoe has entered her car for a new event: the Bathurst Time Trial. Her car (a '61 Holden fitted with tail fins to increase speed) is believed to be so fast that a special timing system has been devised. It works like this: at the start, a laser in the car sends a beam laterally towards an array of mirrors set up at the half-way point of the course, as shown in the two diagrams below (not to scale). The course has length L and the mirrors are at different distances wn from the track, as shown in the sketch. (The mirrors are also at slightly different heights and the beam is spread in the vertical direction so that it can hit all of them, but this detail is unimportant for the following question.)At the finish line, a reflected beam is received by one of a vertical array of detectors fixed to the side of the car. From the height of the detector that received it, one can tell which mirror reflected the beam. The further the reflector is far from the track, then the further light has travelled during the time trial, so the slower the car. The aim in this race is to have a low value of wn.
i) The judges of the race determine that the pulse received by the car at the finish line was reflected by the nth mirror, at a distance wn from the track. From this observation, the judges then calculate their value of the time tjudge taken by Zoe for the event. Derive an expression for tjudge in terms of L, wn and c, the speed of light.
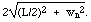 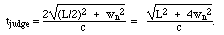
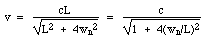 Explain in one or two sentences how you derived your answer.
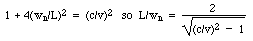 Describe how Zoe (who understands relativity as well as motor mechanics) would explain the difference between the two results for tjudgeand tZoe.
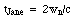
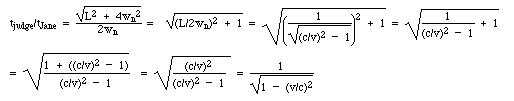
Question 11 (A symmetrical 'twin paradox').Two space travellers are initially at rest, each at a large distance L from a central clock, but in opposite directions. On their twentieth birthdays, each determines that the central clock records the same time. The light has taken the same time to reach each traveller, they are both at rest in the same inertial frame so, in this frame, they are equally old. Complete symmetry.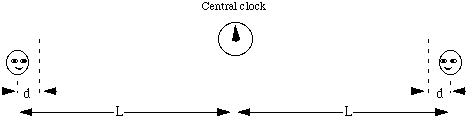 During the unaccelerated flight, they are travelling at relativistic speeds with respect to each other. Consequently, during that part of the trip, each traveller sees that other's clock is running slow, and each sees that the other is ageing more slowly. (And remember that d< Is this a paradox that destroys relativity? If not, why not?
In a frame of reference that is accelerating, you must apply General Relativity. Special Relativity on its own applies only to inertial frames of reference. So Special Relativity alone does not give the right answer in this case. In this case, the twins accelerate from rest and, while they are accelerating, they know that they are not in an inertial frame: they are pushed against their seats by mysterious forces, etc. Yes, one could make d very small, but then the acceleration would have to be greater to achieve relativistic speeds. During the accelerating phase, general relativity must be applied. As we explain in the Twin Paradox, under general relativity, an accelerating frame of reference is locally indistinguishable from a gravitational field. So each twin could see the other as being a height 2L above himself in a uniform gravitational field. At high gravitational potentials, general relativity shows that clocks run more quickly, and the effect is proportional to the potential and so proportional to 2L. (Further, if you make d smaller, then the acceleration to reach the same speed is larger, so the effect is more intense but shorter.) There is also the usual correction for their relative motion (the effect we should get from applying special relativity alone) but, during a sufficiently rapid and distant acceleration, the "special relativity" term (the one that makes clocks run slowly) can be made negligible in comparison with the "general relativity" term (the one that makes clocks run quickly). Both terms are completely symmetrical. Consequently, each twin sees that the other ages rapidly during the acceleration (and the larger L is, the more rapidly the other is seen to age). Then, during the unaccelerated part of the flight, each sees the other age more slowly (the term due to relative velocity, what we could call the "special relativity term", dominates because there is no general relativity term). These two effects cancel out so, when they flash past each other at the central clock, they are the same age. Each agrees that they first fire their rockets simultaneously. Each observed that the other's clock ran more quickly than theirs during the distant acceleration, and then each observed that the other's clock ran more slowly than their own during the unaccelerated phase. Complete symmetry: when they passed each other, they were the same age. Alternatively, if you draw a space time diagram, and include birthday greetings as we did in Twin Paradox, then you will also see that, in all frames, each twin receives the same number of birthday greetings from the other.
It is a neat question, and my correspondent really thought that he'd found an inconsistency in relativity. I also thank this correspondent, who had obviously thought about relativity and who took the time to express the question as elegantly and clearly as possible. (This is not as common as one might hope. See Einstein was wrong.)
However, to all those who feel frustration that Einstein always 'gets away with it' -- that relativity always gives correct and logically consistent answers -- there is this consolation: Despite his important contribution to Quantum Mechanics, Einstein never really accepted the fundamentally stochastic nature of the universe at the small scale. So he posed a series of puzzles to Neils Bohr and others, in which he attempted to show inconsistencies in Quantum Mechanics. In all cases, Einstein's interlocuters were able to show that Quantum Mechanics was right and Einstein was wrong. With co-authors Podalsky and Rosen, Einstein wrote a paper proposing an explicit experiment (the EPR experiment) to test Quantum Mechanics in this way. He did not live to see any of the (approximately equivalent) experiments performed (by Alain Aspect's team in 1982 and by many others since). However, the results are unanimous, and Quantum Mechanics is under no threat -- or at least not from that direction. A nice summary, with links to the original papers, is given by David R. Schneider.
|
Home
| Summary
| Quiz
|
Credits
|
|