Bows and strings
Many of the most useful features of the orchestral string instruments
result from their use of bows. Compared with pizzicato
(plucking the string), the bow allows the player to continuously
input energy and so to maintain a note. This is important to
the timbre, too: after a pluck, the high harmonics fade away
quickly, leaving only the fundamental and some weak lower harmonics.
Bowing maintains the rich harmonic spectrum.
The part of the bow that touches the strings is made of
horsehair (or a synthetic substitute). In the contemporary
bow, the wooden support for the hair is bent towards the hair
— not away from it like an archery bow, or like the violin
bows of the eighteenth century.
This difference in bow shape makes a big difference to playing
and sound. With the old bow, which curved away from the strings,
pushing harder on a string made the bow more curved, so the
ends were closer together. So the force exerted on the string by the hair
doesn't increase rapidly as you push the bow down. With the
modern bow, when the player presses hard on the strings, the
wood straightens, which helps to pull the hair tighter and to allow greater force on the string. Another effect of the modern (Tourte) bow is the presence of the 'hatchet" head, which distributes mor eweight to the tip, allowing a more uniform application of force during the stroke. These effects give the modern bow a greater range of loudness.
The action of the bow which drives the strings is a
regular cycle of stick-slip-stick-slip. This involves
some interesting properties of friction, the force that
makes things difficult to slide. If you have ever tried
to slide a heavy object such as a piece of furniture,
you will know that it is easier to keep it moving than
it is to get it moving in the first place. In this case
static friction (sticking) is greater than kinetic friction
(sliding). This is the case for most dry surfaces. It is
also true of the string and the bow, and the player
puts rosin on the bow to give a big difference between
the two conditions: the coefficient of static friction
is high, while that of sliding friction is very low.
(Note that, in the animation below, the vertical scale
of the string's motion has been magnified, and
the wave speed in the string has been reduced to make the motion visible. There are also many complicating factors (including one due to torsional waves.)
If your browser doesn't support this animation,
see the series of graphics at the foot of the page.
With high static friction, the bow tends to stick to
the string ("stick" in the animation) and for a while
it drags the string along with it. Meanwhile, the kink
in the string travels along the string and reflects
at the fixed end. When the kink returns to meet the
contact point, the tension in the string now acts to
pull the string off the bow. Under appropriate bowing conditions
(that are not easy to learn!), it breaks free of the
bow and then slides past it easily with very little
friction, thanks to the low kinetic friction. This is
the "slip" phase in the animation. The string doesn't
stop when it gets to the straight position because its
momentum carries it on until eventually it stops and
reverses direction. Meanwhile, the kink has travelled
to the near end of the string and reflected back. At
the end of the "slip" phase, it is going at about the
same speed and in the same direction as the bow. At
this point, it catches on the bow again, static friction
reigns, and the cycle begins again. (If any of this is not clear from the animation, compare with the stills at the foot of the page.)
Usually the vibration
of the string governs the cycle of stick-slip: while
the string motion is in the same direction as the bow travel,
it sticks and moves with the bow, when it reverses, it slips.
Thus the cycle of stick and slip on the bow has the
same period as the vibration of the string. This
might be less than a thousandth of a second for a violin
or several hundredths of a second on a double bass.
Do not confuse this cycle with the (much slower) forward and backward
motion of the bow: while the player is moving the bow
in one direction hundreds of stick-slip cycles may occur.(In the animation, only three cycles of stick-slip motion
are shown, to keep the file size acceptable. Further,
it is only an up-bow. When the bow reverses direction,
there is inevitably a small but usually noticeable discontinuity
in the wave motion, which is a key element of the many different types of articulation for string instruments. The bow allows the player to put energy into the vibrating
string and to play long sustained notes. (Animation © Heidi
Hereth)
The bow-string interaction is important in less obvious
ways, too. Over a limited range of force applied by
the player (players call this "pressure"),
the cycle of stick and slip is governed by the standing
wave in the string. (See Waves
in strings.) When this happens the motion of the
string is nearly exactly periodic, and it therefore
makes a sound with an almost
exactly harmonic spectrum. (See also What
is a sound spectrum.) This means that any inharmonic
effects of the string are reduced by bowing, which is
not the case when the string is plucked. The periodic
motion of the string includes rather sudden changes
in direction, and these imply substantial power in the
high harmonics. The regular action of the stick-slip
action thus puts power into the high harmonics and contributes
to the richness, brightness and loudness of the violin's
sound.
|
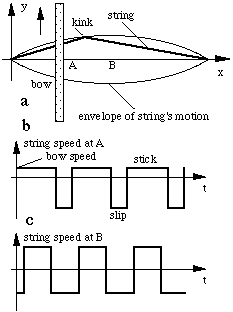Helmholtz motion is the name given
to the idealised motion shown in the animation above.
(Strictly, it occurs only for an idealised, one dimensional
string. Initially, we shan't worry about complications, but we'll mention a couple below).
At all times, the shape of the string is two straight
lines, joined by a kink that travels around the envelope
shown, which is made of two parabolic segments. For a bow moving upwards, the kink travels anti-clockwise,
as shown in the animation. In the graphs of velocity
vs time t, let's say that at the bowing point
(A), an upwards moving bow starts the stick phase at
time t = 0. So at t = 0, v is positive, as shown in
figure b. While the string and bow move together, the
kink travels to the right hand end of the string, reflects
and returns (check this on the animation). When the
kink returns to A, there is a large transient force
on the string (the tension on both sides of the string
now has downwards components). This starts the slip
phase (v < 0 in figure b) during which the kink travels
to the left hand end, is reflected and returns to the
bow, ready to being the stick phase again. At the midpoint
of the string (B), the up and down speeds are equal
(figure c).
Now we can work out the displacement of the string
at the bowing point. The kink travels at a constant
speed V. Let the string's length be L. If the frequency
is f so one cycle takes time 1/f. So the kink travels
2L in time 1/f so V = 2Lf. Suppose we are bowing it
at a position L/n from the closer end, usually the bridge.
During the stick phase, the kink travels to the far
end and back, a distance D = 2L(n-1)/n. At speed V,
this takes a time
D/V = 2L(n-1)/nV = (n-1)/nf.
Now the bow speed is v, so during the stick phase the
bow and the string together travel a distance
where A is the amplitude of the motion of the string at
the bowing point. So, at the same bowing position, the
amplitude of the motion is proportional to the bowing
speed and inversely proportional to the frequency. (In
the animation above, v and f are both very small.) So, if you bow with greater speed, the stick point will travel further and the amplitude will be greater. This of course makes it louder, which is what conductors want when the say "use more bow".
If you vary the bowing position but keep the bow speed
constant, you are changing only n and A in the equation
above. Measuring the bowing position from the closer
end of the string means that n can vary between 2 and
a large number. So the amplitude at the bowing position
increases from v/2f if you bow at the middle, towards
v/f as you get close the bridge. However, the maximum
amplitude of the string's motion is greatest at the
middle. As you move the bowing point towards the bridge,
the maximum amplitude of the string increases for this
reason as well.
The diagram and the explanation above are simplified. See real measurements on this link, which also explains one of the important complications.
|
Bow force comes into this because, for a given bowing
speed and bowing position, there is only a certain range of
bow force that will maintain Helmholtz motion. For a given bowing
speed, the required force is a little higher as you bow closer
to the bridge. Further, the permitted range becomes narrower,
so you must judge the force more accurately. The pay-off is
that, with more applied force, you excite more higher
harmonics so the tone is brighter and richer.
For bowing harmonics, the story is more complicated.
For the second harmonic, there are two cycles of stick slip
in the time that a kink takes to make one complete return
trip along the string. However, there are two kinks travelling
at any time, L/2 apart. Each time one of them arrives at the
bow after a reflection from the distant end, it initiates
a slip. When it arrives from a reflection at the closer end,
it initiates a stick phase. The differences between bowing
the fundamental and bowing the second harmonic are shown in
a graphic at the bottom of the page.
Now let's return to address some of the complications neglected above. A real bowed string never passes through a position
where it is completely straight. Instead, it retains a small displacement at the bow
in the bowing direction. The sharp corner of the kink produces all of the
harmonics, except for those that have a node at the bowing point. However, because a string has a certain
stiffness, the kink is never perfectly sharp and the finite curvature limits the number of upper
harmonics. Bowing with greater force (usually closer to the bridge) gives a sharper kink and therefore more high harmonics and a brighter tone.
For more more information, see
|
