|
|
|
| Relativity
in brief... or in detail.. |
Maxwell's equations: are they really so beautiful that you would dump Newton?Maxwell's equations describe electricity, magnetism, space, time and the relationships among them. They are simple and fundamental. As we saw in the introductory film clip, their simplicity, symmetry and beauty persuaded Einsten to develop a theory of relativity in which Maxwell's equations were invariant. Here we explain why, and derive an expression for the speed of light along the way.
Although the equations are simple, they are notated in a few different ways, for use in different circumstances. The variable quantities are the electric field E (written in bold here to indicate that it is a vector), the magnetic field B, the electric charge density ρ (the amount of charge per unit volume) and the electric current density J (the amount of electric current flowing through unit area). There are also properties of the medium, even if it is vacuum. ε is the dielectric permittivity. It is a property of a medium that determines the strength of the electric field produced by a given electric charge and geometry. Greater values of ε mean that more charge is required to produce the same electric field (for all materials in the liquid or solid phase, ε is greater than the vacuum value ε0). μ is the magnetic permeability of a medium. Greater values of μ mean that a given value of electric current produces a stronger magnetic field (magnetic materials such as iron may have values thousands of times higher than the vacuum value μ0). For our purposes (dealing with light in vacuum) we only need Maxwell's equations for the case of the vacuum, where ε and μ take their (uniform and constant) vacuum values of ε0 and μ0.
Maxwell's equations: integral form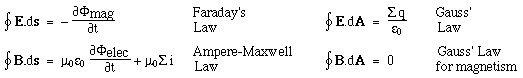 This page poses the author a problem. It is possible to go from here to the wave equation, without using vector calculus. However, to do so would lose the elegance that I wish to stress here. Students usually don't do vector calculus until approximately second year university. Readers who are familiar with vector calculus will probably know Maxwell's equations already. So, for the benefit of many readers who still haven't tasted those pleasures, what I shall do next is to show the equations in their more elegant forms, giving an informal description of the notation. (Formal derivations of the wave equation from either the integral or differential forms are found, of course, in many text books.) The symbol ∇ (pronounced 'del') expresses how strongly a quantity varies in space: it is a sort of spatial derivative. Loosely speaking, if you move in one direction, ∇.E (pronounced 'div E') expresses how much E varies spreads out or how much it changes in that direction. ∇xE (pronounced 'curl E') measures how much E curls around, or how much it changes in the perpendicular directions. This allows us to write:
Maxwell's equations in differential form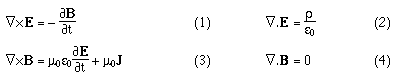 Below we write them in a more symmetric and beautiful form: a form that shows more clearly their various symmetries. However, for the moment, let's put them to use. Maxwell's equations and the speed of lightLet's consider light travelling in a vacuum, ie in a region in which there are no electric charges, so that ρ = 0 and J = 0. Again for the vacuum, Maxwell's equations become: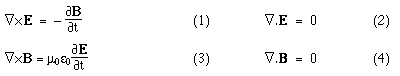 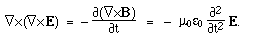 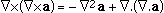 . Here, ∇.E = 0, so . Here, ∇.E = 0, so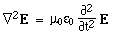 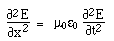 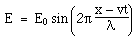 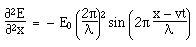 and and 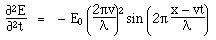 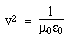 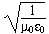 . When Hertz found this solution, he recognised that the value of this quantity was the speed already known for light, which strongly suggested that light was a wave, and part of the electromagnetic spectrum, along with radio. If you're interested, we show film clips of measurements of the speed of light and of (UHF) radio waves in a multimedia tutorial on The Nature of Light. . When Hertz found this solution, he recognised that the value of this quantity was the speed already known for light, which strongly suggested that light was a wave, and part of the electromagnetic spectrum, along with radio. If you're interested, we show film clips of measurements of the speed of light and of (UHF) radio waves in a multimedia tutorial on The Nature of Light.
In a physics lesson, we're not yet finished: we have to check that, associated with this wave in the electric field, there is another in the magnetic field, and that the two together satisfy the equations in three dimensions. But this page is not a (usual) physics lesson and so, as they say, we leave this as an exercise for the reader.
Other forms of Maxwell's equationsNote that the values of ε0 and μ0 relate our units of mechanics, electricity and magnetism. We could choose our system of units such that ε0 = 1 and μ0 = 1. In fact, many theoretical physicists sometimes use these units. They have the effect of making Maxwell's equations even simpler and more symmetrical. (They have the practical disadvantage that other units then have uncomfortable sizes. With c=1 in these units, either the unit of length is very long or (more usually) that of time very short.)Another asymmetry is the appearance of ρ and J in the equations: the electric charge density and electric current density. These arise because individual charges can move independently. In magnetism, a North and South pole always appear together. If there were isolated magnetic monopoles (as Dirac had predicted*), we could define a magnetic charge density ρmag and magnetic current density Jmag. Using grey symbols for the magnetic monopole terms that seem to be zero in our universe, this would give us the following set of Maxwell's equations: Maxwell's equations: symmetric form (with magnetic monopoles and with ε0 = 1 and μ0 = 1)
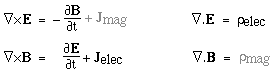 And if you'd like to read a bit more about the practical side of Maxwell's equations and electromagnetism, try The electromagnetic spectrum and the multimedia tutorial on The Nature of Light. * Dirac and the magnetic monopole - a personal anecdote. When I was a student, I remember the thrill of seeing the announcement of a lunchtime lecture to be given by Paul Dirac. Wow, P.A.M. Dirac, one of the greats of quantum mechanics. The Dirac who had predicted the existence of the positron (later found) and the magnetic monopole (later not found). He even has a mathematical function named after him. Then, coincidence: on the morning of the lecture, the newspapers carried reports that a team of physicists had reported evidence that appeared to be consistent with a magnetic monopole. What an exciting coincidence — and we should get the great man's reaction. The theatre was packed when he came in. He would not give the lecture whose title had been announced, he said, because he knew what we wanted to hear. (Applause.) In the decades since he had done the monopole work, I expect that he would have given it little thought: it must have seemed like a lost cause. His notes and papers about it would have been back in Britain. And he would only have had a few hours, at most, to think about it. The theatre was packed and the old man spoke in a quiet voice, but you could have heard a monopole drop as he gave a really clear review of his work, all those years ago. He finished by warning us that he thought that the latest announcement would prove to be a false alarm. He was right. But the lecture remains a treasured memory. Incidentally, with the proceeds from a book made of Dirac's lectures in Australia, the physics school here at UNSW offers a Dirac medal for theoretical physics. Professor Edward Shuryak was the 2004 winner.
|
Home
| Summary
| Quiz
|
Credits
|
|