What is acoustic impedance and why is it
important?
How does a particular fingering (or trombone slide position) help me play a note? And why are some notes brighter or more resonant than others? When you play, resonant sound waves in the instrument collaborate with the reed, airjet or player's lips to produce a note. In sound waves, the pressure and airflow oscillate: this variation is called acoustic pressure and acoustic flow (so don't confuse them with the steady blowing pressure in your mouth and the airflow from your lungs).
To explain the principles involved, we need to discuss the acoustic impedance, which you can think of it as the acoustic
response of the instrument for all possible frequencies. Acoustic impedance has the symbol Z, and is defined as the ratio of acoustic pressure p to acoustic volume flow U. So we define Z = p/U. High Z means that a small acoustic flow generates (or requires) a large pressure: good for driving a reed or lips; small Z means the reverse: good for driving an airjet in and out of a flute blowhole. In an instrument, the magnitude of Z varies strongly (by a factor of 1000 or so) when you scan through the frequency.
For
musical wind instruments, acoustic impedance has the advantage
of being a physical property of the instrument alone – it
can be measured (or calculated) for the instrument without
a player. It is a spectrum, because it has different values
for different frequencies. When we measure it at the mouthpiece of an instrument, it tells us a lot about the way the player's lips,
reed or the air jet from the mouth will interact with the
instrument itself. So it tells us about the acoustic performance
of the instrument, in an objective way that is independent
of who might play it, and it allows us to compare subtle differences
between instruments. So what is it?
An analogy. Many people find helpful the analogy with electrical impedance. Spatial variations in electrical potential (differences in voltage V) give rise to moving charge (electrical current i) and the electrical impedance Z = V/i. Here, spatial variations in acoustic pressure (p) give rise to air flow (U) and Z = p/U. Here is an introduction to electrical impedance. Resistance is a particular (and rather boring)
example of impedance, which is the general term for
a ratio of voltage to current. DC (direct
current) means constant or slowly varying current. AC
(alternating
current) means any current in which the movement is alternately
backwards and forwards (oscillating) with no overall motion.
AC is more interesting because the impedance can vary with
the frequency of oscillation of the current. (These analogies
are limited: air is compressible so the flow does not
obey Kirchoff's law about conservation of current.) A more formal explanation is given in Sound: impedance, power and intensity. For a review of measurement techniques, see Dickens et al (2007).
|
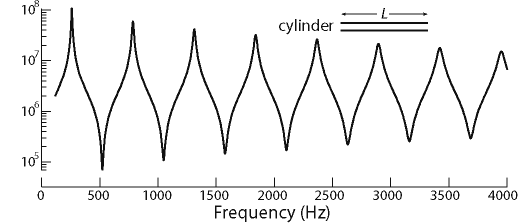The graph shows the measured impedance of a simple cylindrical pipe
(325 mm long, 15 mm in diameter) in Pa.s/m3, as a function of frequency. Don't be misled by the compressed (log) scale: the magnitude of Z varies by more than a factor of a thousand over this range of frequency. More about this below.
The acoustic impedance is complicated by the fact that the current
and pressure are not necessarily in phase – the maximum pressure
may be ahead of the maximum flow, or vice versa. As in
electricity, we use complex numbers to handle this, where
the real part represents the in-phase component and the imaginary
part the out-of-phase component.
Units. The unit of pressure is the pascal – one Pa or one
newton per square metre. A pascal is a big unit for sound:
an oscillation of one Pa is usually a very loud sound indeed.
(In DC the Pa seems a small unit: atmospheric pressure is
100,000 Pa or 100 kPa.) Flow is measured in cubic metres per
second. (A very gentle breeze coming in your window could
be 1 m3/s. But for 1 m3/s to flow down
a pipe, either the pipe must be big – think ventilation ducts
– or the speed must be high.) The simplest unit for impedance is the Pa.s/m3, which we call the acoustic ohm, Ω. For musical instruments, it
is a rather small unit, so we use megohms: MPa.s/m3.
Finally, sound pressures have a large range. For this and
other, psychophysical reasons we use logarithmic scales for
sound level and impedance. |
|
 If we send a sound wave into a pipe, the wave reflects at the far end (whether
closed or open) and comes back, reflects again, and
gives rise to standing waves or resonances (see pipes
and harmonics). This causes the impedance to be much higher
or lower than the value calculated above, depending on whether
the pressure of the returning wave is in phase or out of phase
with the driving pressure.
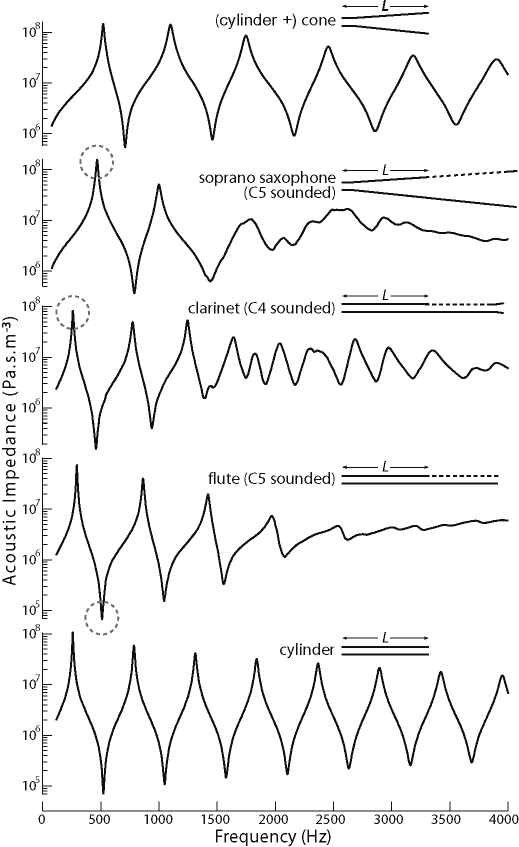
The figure at right (from a paper by Chen et al, 2009) shows the measured impedance spectra for a cylinder (bottom), a flute, a clarinet, a soprano saxophone and a cone (whose apex is replaced by a cylindridal section of the same volume, so as to allow a measurement). In all cases, the impedance becomes small at very low frequency: little pressure difference is required to pump air through a short pipe at low frequency. The first peak corresponds to the frequency of the animation shown on the web page about cylindrical pipes.
The acoustic impedance of musical wind instruments varies spectacularly with frequency because these instruments
are designed to produce one or several frequencies only in
a particular configuration. For example, the flute is played
with the embouchure hole (at least partly) open to the atmosphere,
so the pressure at the embouchure hole is very near to atmospheric
pressure. Thus the acoustic pressure (the varying part) is
nearly zero. The flow is provided by a jet of air from between
the player's lips. Oscillations of air flow in the flute can
cause this jet to deflect upwards (outside the flute) or downwards
(inside) so that the acoustic flow (the AC component) can
be large. Thus the flute operates at minima of Z: a
small pressure and a large flow. Most other wind instruments
have a reed which is sealed by the player's mouth and they
operate at maxima of Z: the varying part of the pressure
is large, but the oscillating part of the air flow is small
at the reed. See Flutes
vs Clarinets and Pipes and resonances for more details to examine simple cases. Many examples of impedance spectra are given on our sites for the flute, the clarinet, the saxophone and brass instruments.
In each of the impedance curves for the flute, there are
at least a few rather deep, sharp minima, and the flute will
usually play a note with a frequency near each of those deep
minima. The ease of playing and the stability of the note
depend on the depth and narrowness of the minima.
Conversely, in each of the impedance curves for the clarinet, saxophone and brass instruments,
there are at least a few rather high, sharp maxima, and those instruments will often play a note with a frequency near each
of those high maxima. The ease of playing and the stability
of the note depend on the height and narrowness of the maxima.
For instance the very highest notes are hard to play, and
you can see on the spectra that at high frequency the maxima
and minima are weaker—they "help the player less". There
is more to it than this, however. For the instrument to play
properly a note with frequency f, it sometimes needs an extremum
at f, and also extrema at 2f, 3f, 4f etc. The reason for this
is that the vibration of the air jet or reed and the sound
made by the flute are not simple sine waves. Their waves are
periodic waves (that is they repeat in time) and they contain
a fundamental and a harmonic series. It is important to the
performance of wind instruments that the various minima that
help produce a particular note are in the harmonic series.
See "How
harmonic are harmonics?" and "How
do woodwind instruments work?"
On our sites for the flute, clarinet and saxophone, it is helpful to look at the Z curve for
the lowest note for an explanation of some of the general features of that instrument's impedance spectrum.
|
Why is Acoustic Impedance Important?
The acoustic impedance of an instrument for any particular
fingering is one of the major factors which determines the acoustic
response of the instrument in that fingering. It determines which
notes can be played with that fingering, how stable they are
and it also helps determine whether they are in tune.
The acoustic impedance also has a
large influence on the sound produced. To see some examples
of this, have a look at the two different fingerings for the
same note. On the flute, one could look at A#4
(the "long" fingering using the RH index finger, and the "short"
fingering using only the LH thumb). Look in particular at
the relative depths of the 3rd and 5th minima in the impedance
spectrum, and at the strengths of the 3rd and 5th harmonics
of the sound produced. Look also at the two different fingerings
given for A4,
the relative depths of the harmonic minima, and the effect
that they have on the timbre produced. Another difference
that is worth looking at is the difference made by a "split
E" mechanism. Look at the different Z spectra for E6
with and without the mechanism, and compare them with that
for the note A5.
Then try the experiment of slurring between A5 and E6 on flutes
with and without the mechanism.
Our databases for clarinet and saxophone also provide many examples.
Another thing which has a big influence on the sound is
the player, but that is another story and it is rather more
complicated. Indeed a big advantage in measuring Z is that
it gives us an objective measurement of the instrument alone.
In that way it is in some ways more useful to scientists and
to makers than the sound of the instrument. If you get
a poor sound from an instrument, it might be because the player
is poor, or it might be because the instrument is poor. With
our industrial collaborators, Terry
McGee and The
Woodwind Group, we are working to obtain objective comparisons
of different instruments, to analyse the differences in their acoustic
properties and to explain their different musical performance.
More about acoustic impedance |
