Bore angles and standing waves
Wind instruments rely on standing waves in the bore, and the standing waves require reflections at both ends (see this page for explanation). For a cone (we’ll neglect the modest bells for now), the reflection at the output is weaker for a large output diameter. This is particularly true for high frequencies, which are radiated better than low. Or, more formally, consider that the radiation impedance goes as f/r and that the characteristic impedance of a duct goes as 1/r2; so that the ratio of radiation to characteristic impedance goes as rf (or r/λ). So reflection is weaker for large aperture and for high frequency. (Informally, one might think of this as going from a limited space into a large one, and the reflection depending on the difference.)
So waves are radiated better for a large output radius. This makes the instrument with a large cone angle louder – which was one objective Adolphe Sax had when he invented the saxophone. Further, higher frequencies are radiated better than low (for all angles).
Radiation, bore angle and the cut-off frequency
 But more radiation means less reflection for wide bore instruments. This lower reflection reduces the strength of the standing waves in the bore. In practice, the effect of the cone angle is complicated by the tone-hole cut-off effect: the cut-off frequency is higher in the saxophones than in oboes and bassoons. An estimate of the cut-off frequency is
But more radiation means less reflection for wide bore instruments. This lower reflection reduces the strength of the standing waves in the bore. In practice, the effect of the cone angle is complicated by the tone-hole cut-off effect: the cut-off frequency is higher in the saxophones than in oboes and bassoons. An estimate of the cut-off frequency is
where b is the radius of a typical tone-hole, a the radius of the bore, v the speed of sound, s is half the typical spacing between tone holes and t the typical effective length of the tone hole, including end effects. See this page for more detail.
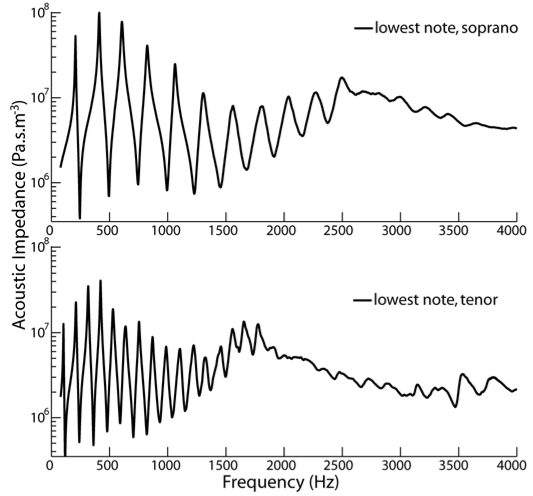
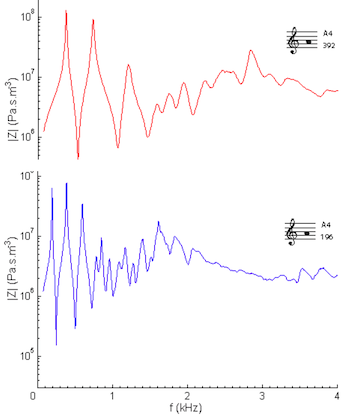
The combined behaviour of cone angle and cut-off can be observed in the impedance spectra measurements for soprano and tenor sax – and compared: the soprano has a larger angle. The effect of cone angle alone can be compared in the measurements of the (atypical) lowest note. A few example spectra are shown below.
Effect on registers
The large bore angle is one of the important differences between the saxophone and the bassoon. Similarly, the bore angle is an important difference between the oboe and the soprano sax, with the tarogato as a compromise. (The single vs double reed is another, of course.)
The narrower cone means that the bassoon can play well over three octaves without using the vocal tract. (The Rite of Spring and Shostakovich IX both call for D5.) The tenor sax can comfortably match this upper range, but its low note is Ab2, compared with the bassoon’s Bb1. (Incidentally, for bassoon parts written in the tenor clef, a tenor sax can read the part at pitch, pretending it is treble clef, and the bassoon parts written in bass clef can likewise be read by baritone sax, which almost covers the low range of the bassoon.)
The graphs below come from a large collection impedance spectra measurements for soprano and tenor sax