Acoustics of bell plates
This page is an appendix for the scientific paper :
Lavan, D., Hogg, S. and Wolfe, J. (2003) "Why
do bell plates ring?" Acoustics
Australia, 31, 55-58,
and vice versa.
 |
Bell plates (sold commercially
as Belleplates) are metal plates that, when struck,
ring with a strong initial transient, followed
by a nearly pure decaying sinusoidal tone. They
are played like handbells but are rather cheaper
and less loud. One might say that their sound is sweeter but less interesting than that of handbells.
The photo shows three plates:
the first two are in the standard shape used
for bell plates, the third is an equilateral
triangle with a tang at one corner. The beaters
used to make the sound files below are shown:
a soft fabric beater, a soft rubber mallet and
a hard rubber mallet.
These three shapes all play well, that is to say
they all ring for tens of seconds when struck.
However, as we shall see below, only a limited
class of shapes works for bell plates: in general,
polygons with a handle at one corner just go
'clunk'.
|
|
In the photographs above, the shape of the largest plate
is shown in comparison with those of the others. As
expected, the smaller plate is higher in pitch than
the larger plate of the same shape. The equilateral
plate is interesting because, as well as the principal
mode, there is another sounding mode at about three
times the frequency (a twelfth higher in pitch), which
fades more rapidly than the principal mode. This higher
mode is the ring mode of the equilateral triangle. One
can, however, strike the plate at a node of the higher
mode and thus obtain just the lower tone. Perhaps this
complication is one reason why the equilateral plate
is not used in commercial instruments. The shape
of bell plates is important to the sound. We demonstrate
this by progressively slicing strips off the end of
a plate, recording the sound for each shape. We then
slice vertical strips off the corners until we regain
the initial shape. The soft rubber mallet is used
in all sound files.
We now start taking slices off the corners, to return
to the original proportions.
So why is the shape critical?
In the paper
on bell plate acoustics, we explain that, for the
conventional bell plate shape, the two nodes of the
(0,2) mode converge at the tang, where the plate would be held to play. This is not true for
general shapes. We give a summary of the argument here.
(For an introduction to modes of vibration of plates,
see Chladni
patterns.)
Consider the two simplest modes of
vibration of a rectangular plate. These are named
according to the numbers of nodes parallel to the
short and long axes respectively: (0,2) and (2,0).
Their Chladni patterns are shown below. The pale lines
are nodes: lines of no displacement. areas on either
side of a nodal line move in opposite directions.
Because it is easier to bend a regtangle about its
short axis than about its long, the (0,2) mode has
the lower frequency. (What happens for a square, when
the (0,2) and (2,0) mode have the same frequency?
If you add these two vibrations together in phase,
you get the mode shown in the third photograph.)
.GIF)
.GIF)

These (2.0) and (0,2) modes are sketched below.
Cross sections along the lines a-a' and b-b' are sketched
to show the shape at two instants separated by half
a cycle.
(2,0).GIF)
The lower half of the figure shows the analogous
modes of a bell plate. The (2,0) mode (left) is the
more important. If we imagine cutting away the corners
of a rectangular plate, we move the nodal lines closer
towards the centre. Eventually they intersect. This
is the shape used for bell plates.
Now at a nodal line, the position of the plate isn't
changing. So a node is the place to hold a plate if
you want it to ring. However, on either side of the
node, the plate is moving in opposite directions,
so the plate is rotating locally. (See the cross sections
in the sketches above.) If you hold a plate with your
fingers at a simple nodal line, as we do in an example
below, you damp the sound a little.
At the intersection of two nodal lines, there is
no rotation: both displacement and slope are zero.
This is the place to put the handle, which becomes
an extended node itself. Let's see how this works:
 |
A. Here I am
holding it at the normal position, which is an
extended region formed from the fusion of the
two nodes of the (2,0) mode. 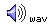

|
|
 |
B. Here I'm
holding it at a point on one of the nodes of the
(2,0) mode. Still the same mode, so it has the
same pitch. But because it is a simple node, rather
than the intersection of two nodes, the plate
is rotating locally about this node. This rotation
transfers energy to my fingers, so it rings for
a shorter time. 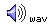
 |
|
 |
C. This point
is an antinode of the (2,0) mode but a node of
the (0,2), so of course it is the latter mode that
sounds: about one tone lower than the (2,0).
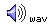

| |
 |
D. This point
is at the intersection of a node of the (0,2)
and a node of the (0,2). So, by striking at a
point that is not a node of either, it is possible
to sound the two modes together. (In B above,
I also held it at this point, but struck at a
node of the (0,2), so only the (2,0) sounded).
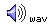

The finger and thumb damp both modes, so the
interference between the two modes is not very
clear. So... |
|
 |
E. Here the
plate is suspended by a thread through a hole
drilled at the intersection of the two nodes.
The local rotation of each mode transfers rather
little energy to the thread, so the plate rings
in both modes. The transients are clearer too.
Notice that the interaction of several different
modes that are not harmonically related makes
the sound more like that of a bell. 

|
|
How does the sound depend on direction?
|

